
The other statistics compare the empirical distribution function to the fitted CDF in different ways. The Kolmogorov-Smirnov test computes the maximum distance between the cumulative distribution of RAND35 and the CDF of the fitted distribution.


The chi-square test divides the range of RAND35 into nonoverlapping intervals and compares the number of observations in each class to the number expected based on the fitted distribution. This pane shows the results of tests run to determine whether RAND35 can be adequately modeled by various distributions. P-values less than 0,05 would indicate that RAND29 does not come from the selected distribution with 95% confidence. The Kolmogorov-Smirnov test computes the maximum distance between the cumulative distribution of RAND29 and the CDF of the fitted distribution. The chi-square test divides the range of RAND29 into nonoverlapping intervals and compares the number of observations in each class to the number expected based on the fitted distribution. This pane shows the results of tests run to determine whether RAND29 can be adequately modeled by various distributions. P-values less than 0,05 would indicate that RAND27 does not come from the selected distribution with 95% confidence. The Kolmogorov-Smirnov test computes the maximum distance between the cumulative distribution of RAND27 and the CDF of the fitted distribution. The chi-square test divides the range of RAND27 into nonoverlapping intervals and compares the number of observations in each class to the number expected based on the fitted distribution. This pane shows the results of tests run to determine whether RAND27 can be adequately modeled by various distributions. Other P-values are based on general tables and may be very conservative (except for the Chi-Square Test). Then add all the probabilities using sum() function and store the result in result4.*Indicates that the P-Value has been compared to tables of critical values specially constructed for fitting the selected distribution. The first command compute the Geometric probability for $x=3$, $x=4$ and $x=5$. The above probability can also be calculated using dgeom() function along with sum() function. The above probability can be calculated using pgeom() function as follows: result3 <- pgeom(5,prob)-pgeom(2,prob) Then the probability distribution of $X$ is Geometric distribution is used to model the situation where we are interested in finding the probability of number failures before first success or number of trials (attempts) to get first success in a repeated mutually independent Beronulli's trials, each with probability of success p
GEOMETRIC CDF HOW TO
In this tutorial, you will learn about how to use dgeom(), pgeom(), qgeom() and rgeom() functions in R programming language to compute the individual probabilities, cumulative probabilities, quantiles and to generate random sample for Geometric distribution.īefore we discuss R functions for Geometric distribution, let us see what is Geometric distribution.
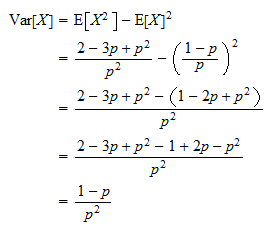
4.3 Example 2 Visualize Geometric probability distribution.4.2 Example 1: How to use dgeom() function in R?.4 Numerical Problem for Geometric Distribution.3 Geometric probabilities using dgeom() function in R.1 Geometric distribution probabilities using R.


 0 kommentar(er)
0 kommentar(er)
